正整数、负整数和0统称为整数。整数的个数是无限的,没有最小的整数和最大的整数。

一、整数的分类和意义
1.自然数的含义:自然数源于数数,在数物体的时候,用来表示物体个数的1,2,3,…99,100…都叫做自然数。一个物体也没有,用0表示(0也是自然数)。
最小的自然数是0,最小的一位数是1,自然数的单位是1。
2.自然数(0除外)的两方面意义
(1)用来表示事物多少的叫基数。例:"7本书"中的"7"是基数;
(2)用来表示事物次序(顺序)的叫序数。例:"第9天"中的"9"是序数。
3.0的意义(0的作用)
(1)在计数时0起占位作用,表示该位上没有单位;
(2)表示起点,如零刻度;
(3)计数,如果一个物体也没有,用0表示;
(4)表示界线,如温度计,数轴上的0,表示正、负数的分界线;
(5)0是一个完全有确定意义的数;
(6)0不能作除法的除数、分数的分母、比的后项;
(7)0是最小的自然数,是一个偶数;是任何自然数(0除外)的倍数。
4.整数的含义
像-5,-2,0,2,5,10,……这样的数统称整数。整数的个数是无限的,没有最小的整数,也没有最大的整数。
(1)正整数:大于0的自然数或整数。
(2)负整数:像-1,-2,-3,……这样的数叫做负整数。它是与正整数表示相反意义的量。(小于0的整数。)
(3)0既不是正数也不是负数,它是最小的自然数。1是最小的一位数。
5.整数的分类
6.正数和负数
(1)正数的含义
像以前学过的+1、+200、+、+4.8、+24%,……这样的数叫做正数。正数前面的"+"号,称为正号,也可以省去不写。
(2)负数的含义
小于0的数叫做负数。像-5、-7.8、-、-500、-35%,……这样的数都是负数。
7.负数在日常生活中的应用
正、负数是表示两种具有相反意义的量。如:收入与支出、海平面以上与海平面以下、零下与零上、盈利与盈亏、左与右、东与西、余钱与亏钱、进与出、增产与减产、得分与扣分、上升与下降等。
二、整数的读写
1.数位顺序表
(1)数级:从个位起每四位是一级,依次是个级、万级、亿级……。
个级表示多少个一,计数单位"一";万级表示多少个万,计数单位"万";亿级表示多少个亿,计数单位"亿"。
(2)位数:一个数含有数位的个数叫做位数。因此,在一个数中所含数字的个数是几,这个数就叫做几位数。
(3)数位:各个计数单位所占的位置,叫做数位。数位是按固定顺序排列的。
(4)计数单位:整数和小数都是按照十进制计数法写出的数,其中个、十、百……以及十分之一、百分之一……都是计数单位。它表示各个数位上的一个1表示的是多少。
2.整数的读法:从高位到低位,一级一级地读。读亿级、万级时,按照个级的读法去读,只要在后面加一个"亿"或"万"字就可以了。每一级末尾的0都不读出来,级首或级中有一个或连续几个0,都只读一个零。
读数和写数时,如果数的后面有单位名称,则单位名称不能丢掉。
3.整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
4.整数的大小比较
(1)比较两个数的大小,如果位数不同,那么位数多的那个数就大。
(2)如果位数相同,先看最高位,最高位上的数大那个数就大;最高位上的数相同,次高位上的数大那个数就大,如果还相同,则继续依次比较,直到比较出大小为止。
5.整数的改写和近似数
一个较大的多位数,为了读写方便,常常把它改写成用"万"或"亿"作单位的数。有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
(1)整数的改写
准确数:在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数。改写后的数是原数的准确数,根据需要还可以还原。例如把1254300000改写成以万作单位的数是125430万;改写成以亿作单位的数是12.543亿。
(2)近似数
用一个与它比较接近的数来表示事物的数量,这样的数就是近似数。(根据实际需要,我们还可以把一个较大的数,省略某一位后面的尾数,用一个近似数来表示。)例如:1302490015省略亿后面的尾数是13亿。
近似数常用词:精确到哪位小数、保留几位小数等。
a.四舍五入法:要省略的尾数的最高位上的数是4或者比4小,就把尾数去掉;如果尾数的最高位上的数是5或者比5大,就把尾数舍去,并向它的前一位进1。例如:省略345900万后面的尾数约是35万。省略4725097420亿后面的尾数约是47亿。
b.进一法:在取近似数时,不管多余部分上的数量是多少,都向前进1。这种求近似数的方法,叫做进一法。
c.去尾法:在取近似数时,不管多余部分上的数量是多少,一概去掉。这种求近似数的方法,叫做去尾法。
整除特征
1. 若一个数的末位是单偶数,则这个数能被2整除。
2. 若一个数的数字和能被3整除,则这个整数能被3整除。
3. 若一个数的末尾两位数能被4整除,则这个数能被4整除。
4. 若一个数的末位是0或5,则这个数能被5整除。
5. 若一个数能被2和3整除,则这个数能被6整除。
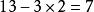
6. 若一个数的个位数字截去,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除。如果差太大或心算不易看出是否7的倍数,就需要继续上述「截尾、倍大、相减、验差」的过程,直到能清楚判断为止。例如,判断133是否7的倍数的过程如下:,所以133是7 的倍数;又例如判断6139是否7的倍数的过程如下:,,所以6139是7的倍数,余类推。
7. 若一个数的未尾三位数能被8整除,则这个数能被8整除。
8. 若一个数的数字和能被9整除,则这个整数能被9整除。
9. 若一个数的末位是0,则这个数能被10整除。
10. 若一个数的奇位数字之和与偶位数字之和的差能被11整除,则这个数能被11整除。11的倍数检验法也可用上述检查7的「割尾法」处理。过程唯一不同的是:倍数不是2而是1。
11. 若一个数能被3和4整除,则这个数能被12整除。
12. 若一个数的个位数字截去,再从余下的数中,加上个位数的4倍,如果和是13的倍数,则原数能被13整除。如果差太大或心算不易看出是否13的倍数,则重复「截尾、倍大、相减、验差」的过程,直到能清楚判断为止。
13. 若一个数的个位数字截去,再从余下的数中,减去个位数的5倍,如果差是17的倍数,则原数能被17整除。如果差太大或心算不易看出是否17的倍数,同样重复之前的过程,直到能清楚判断为止。
14. 若一个数的个位数字截去,再从余下的数中,加上个位数的2倍,如果差是19的倍数,则原数能被19整除。如果差太大或心算不易看出是否19的倍数,同样重复之前的计算思路,直到能清楚判断为止。
15. 若一个数的末三位与3倍的前面的隔出数的差能被17整除,则这个数能被17整除。
16. 若一个数的末三位与7倍的前面的隔出数的差能被19整除,则这个数能被19整除。
17. 若一个数的末四位与前面5倍的隔出数的差能被23(或29)整除,则这个数能被23整除


























































































